Trigonometry Practice Problems for the ACT
This page has trigonometry practice problems and concepts for you to study, such as sine, cosine, and tangent.
$\text{cosine = } \dfrac{adjacent}{hypotenuse}$
$\text{sine = } \dfrac{opposite}{hypotenuse}$
$\text{tangent = } \dfrac{opposite}{adjacent}$
How to Calculate Cosine
Cosine can be calculated as a fraction, expressed as “adjacent over hypotenuse.”
The length of the adjacent side is in the numerator and the length of the hypotenuse is in the denominator.
$ \text{cosine = } \dfrac{adjacent}{hypotenuse}$
Cosine of Angle a
In the illustration below , side Y is the hypotenuse since it is on the other side of the right angle.
The adjacent side is side X because it is next to angle a. 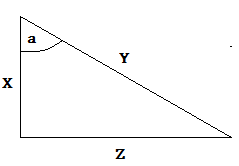
So, the formula for cos of angle a for the above practice problem is:
$ \text{cosine = } \dfrac{adjacent}{hypotenuse}$
$ \text{cosine a = } \dfrac{X}{Y}$
Cosine of Angle b
If you change the angle that you are measuring, the adjacent side will be different.
Suppose we want to measure the cosine of the other angle (angle b) in our example triangle.
In the illustration below, the adjacent side is now side Z because it is next to angle b.
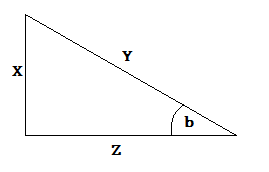
So, the formula for cos of angle b is:
$ \text{cosine = } \dfrac{adjacent}{hypotenuse}$
$ \text{cosine b = } \dfrac{Z}{Y}$
Cosine Rules
Remember the following useful trigonometric formulas. They are valid with respect to any angle:
sin2 + cos2 = 1 cos2
cos2 = 1 – sin2
sin2 = 1 – cos2
Calculating Sine
You will need to know how to use sine in trigonometry practice problems on for the ACT.
When expressed in the form of a fraction, sine is calculated as “opposite over hypotenuse.”
The length of the opposite side goes in the numerator and the length of the hypotenuse goes in the denominator.
$ \text{sine = } \dfrac{opposite}{hypotenuse}$
Sine of Angle a
As in our illustration of cosine, side Y is the hypotenuse in our triangle since side Y is across from the right angle.
The side that is opposite to angle a is side Z because side Z is directly across from angle a.
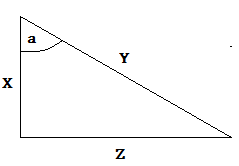
So, the sine of angle a in our illustration above is calculated as follows:
$ \text{sine = } \dfrac{opposite}{hypotenuse}$
$ \text{sine a = } \dfrac{Z}{Y}$
Sine of Angle b
If you measure a different angle, the opposite side will change.
Let’s look at the sine of angle b in our example triangle.
In the illustration below, the opposite side is now side X because it is opposite to angle b.

So, the formula for sin of angle b is:
$ \text{sine = } \dfrac{opposite}{hypotenuse}$
$ \text{sine b = } \dfrac{X}{Y}$
Formula for Tangent
Tangent is calculated as “opposite over adjacent.”
So in our fraction, the length of the opposite side is placed in the numerator and the length of the adjacent side is placed in the denominator.
$ \text{tangent = } \dfrac{opposite}{adjacent}$
Tangent of Angle a
In the illustration below, side Z is the opposite side since it is on the other side of angle a.
The adjacent side is side X because it is next to angle a and it is not the hypotenuse.

So, the formula for tan of angle a is:
$ \text{tangent = } \dfrac{opposite}{adjacent}$
$ \text{tan a = } \dfrac{Z}{X}$
Tangent of Angle b
Let’s look at how to calculate the tangent of angle b in our example triangle.
In the illustration below, side X is the opposite side since it is on the other side of angle b.
The adjacent side is side Z because it is next to angle b and it is not the hypotenuse.

So, the formula for tan of angle b is:
$ \text{tangent = } \dfrac{opposite}{adjacent}$
$ \text{tan b = } \dfrac{X}{Z}$
Trigonometric Relationships
These are the trigonometric relationships for right triangles:
- cos2 A + sin2 A = 1
- cos2 A = 1 − sin2 A
- sin2 A = 1 − cos2 A
- tangent = sin ÷ cos.
The trigonometry equations for sine, cosine, and tangent are also included in our ACT formula sheet.
Trigonometry on the ACT – Theoretical Questions
You will see different types of questions on sine, cosine, and tangent on the test.
Some of these problems will tell you directly that you need to calculate the sine, cosine, or tangent.
Example 1: How is the tangent of x calculated?
Other trigonometry questions will be theoretical, like the one below.
Example 2: For any given angle A, sin2 A = ?
ACT Trigonometry – Advanced Practice Problems
You may also need to use trigonometry to solve advanced problems on the test.
For example, the question might show you a triangle and give you the measurements of the degrees of two of the angles in the triangle, and then ask you to calculate the length of one of the sides of the triangle.
More complex problems will show two triangles embedded inside or partially within each other.
In these cases, you will need to use the trigonometry equations you have learned in order to calculate the degrees or length of the particular part of one of the triangles, and then use that result in another calculation for the second triangle in order to arrive at your final answer.
You will also need to use trigonometry equations in order to understand trigonometric graphing and modeling.
Math Equations – Radians
Here are some useful formulas for radians. You can practice these concepts in our math practice test.
Radians:
θ = s ÷ r [where θ = the radians of the subtended angle; s = arc length; and r = radius]
π × 2 × radians = 360°
π × radians = 180°
π ÷ 2 × radians = 90°
π ÷ 4 × radians = 45°
π ÷ 6 × radians = 30°
If you are taking the ACT, you should also visit our geometry section.
